1504. 统计全 1 子矩形

题目

给你一个 m x n 的二进制矩阵 mat ，请你返回有多少个 子矩形 的元素全部都是 1 。

示例 1：

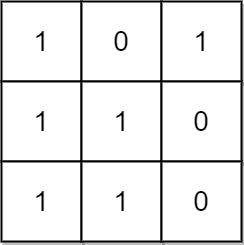
输入：mat = [[1,0,1],[1,1,0],[1,1,0]]
输出：13
解释：
有 6 个 1x1 的矩形。
有 2 个 1x2 的矩形。
有 3 个 2x1 的矩形。
有 1 个 2x2 的矩形。
有 1 个 3x1 的矩形。
矩形数目总共 = 6 + 2 + 3 + 1 + 1 = 13 。

示例 2：

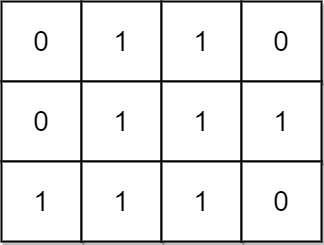
输入：mat = [[0,1,1,0],[0,1,1,1],[1,1,1,0]]
输出：24
解释：
有 8 个 1x1 的子矩形。
有 5 个 1x2 的子矩形。
有 2 个 1x3 的子矩形。
有 4 个 2x1 的子矩形。
有 2 个 2x2 的子矩形。
有 2 个 3x1 的子矩形。
有 1 个 3x2 的子矩形。
矩形数目总共 = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24 。

提示：

• 1 <= m, n <= 150

• mat[i][j] 仅包含 0 或 1

题解

Python

class Solution:
    def numSubmat(self, mat: List[List[int]]) -> int:
        # m 是矩阵的行数，n 是矩阵的列数
        m, n = len(mat), len(mat[0])
        # ans 用于累计所有符合条件的子矩形数量
        ans = 0
        
        # 外层循环：枚举矩形的顶部行（top 为顶行索引）
        for top in range(m):
            # a 数组用于记录每一列在当前 [top, bottom] 范围内的 1 的累计数量
            # 初始化为 0，随着 bottom 向下扩展而更新
            a = [0] * n
            
            # 中层循环：枚举矩形的底部行（bottom 为底行索引，从 top 开始向下扩展）
            for bottom in range(top, m):
                # 当前矩形的高度 h = 底行 - 顶行 + 1（行数）
                h = bottom - top + 1
                # last 记录最近一个不满足「当前列在 [top, bottom] 范围内全为 1」的列索引
                # 初始值为 -1（表示在第 0 列之前没有不满足的列）
                last = -1
                
                # 内层循环：遍历每一列，计算当前高度下可形成的矩形数量
                for j in range(n):
                    # 更新 a[j]：累加当前 bottom 行第 j 列的元素（0 或 1）
                    # 此时 a[j] 表示第 j 列从 top 到 bottom 行的 1 的总数量
                    a[j] += mat[bottom][j]
                    
                    # 判断第 j 列在 [top, bottom] 范围内是否全为 1：
                    # 若 a[j] == h，说明这 h 行中第 j 列都是 1（因为每行加 1，h 行总和为 h）
                    # 若不等，则说明存在 0，更新 last 为当前列索引
                    if a[j] != h:
                        last = j
                    else:
                        # 若当前列满足全为 1，则以 j 为右边界的矩形数量 = j - last
                        # 例如：last=-1, j=2 时，有 3 个矩形（右边界为2，左边界可0/1/2）
                        ans += j - last
        
        # 返回所有子矩形的总数量
        return ans

C++

#include <vector>
using namespace std;

class Solution {
public:
    /**
     * 计算二进制矩阵中所有由1组成的子矩形的数量
     * @param mat 输入的二进制矩阵（元素为0或1）
     * @return 所有全1子矩形的总数
     */
    int numSubmat(vector<vector<int>>& mat) {
        // 获取矩阵的行数m和列数n
        int m = mat.size(), n = mat[0].size();
        // 用于累计所有符合条件的子矩形数量
        int ans = 0;
        
        // 外层循环：枚举矩形的顶部行（top为顶行索引）
        for (int top = 0; top < m; top++) {
            // a数组用于记录每一列在当前[top, bottom]范围内1的累计数量
            vector<int> a(n);
            
            // 中层循环：枚举矩形的底部行（从top开始向下扩展）
            for (int bottom = top; bottom < m; bottom++) {
                // 当前矩形的高度h = 底行 - 顶行 + 1（行数）
                int h = bottom - top + 1;
                // last记录最近一个不满足"当前列在[top, bottom]范围内全为1"的列索引
                // 初始值为-1，表示在第0列之前没有不满足的列
                int last = -1;
                
                // 内层循环：遍历每一列，计算当前高度下可形成的矩形数量
                for (int j = 0; j < n; j++) {
                    // 更新a[j]：累加当前bottom行第j列的元素（0或1）
                    // 此时a[j]表示第j列从top到bottom行的1的总数量
                    a[j] += mat[bottom][j];
                    
                    // 判断第j列在[top, bottom]范围内是否全为1：
                    // 若a[j] == h，说明这h行中第j列都是1（因为每行加1，h行总和为h）
                    // 若不等，则说明存在0，更新last为当前列索引
                    if (a[j] != h) {
                        last = j;
                    } else {
                        // 若当前列满足全为1，则以j为右边界的矩形数量 = j - last
                        // 例如：last=-1, j=2时，有3个矩形（右边界为2，左边界可0/1/2）
                        ans += j - last;
                    }
                }
            }
        }
        
        // 返回所有子矩形的总数量
        return ans;
    }
};